Most Popular Tutorials
Most Popular Tutorials :-

Simply Easy Learning at Your Fingertips. Click Tutorials Menu to view More Tutorial List





What is Number System?

Number System ssssss :-

A computer can understand only a few symbols called digits and these symbols describe different values depending on the position they hold in the number. When we type some letters or words, the computer translates them in numbers as computers can understand only numbers. A computer can understand the positional number system where there are only a few symbols called digits and these symbols represent different values depending on the position they occupy in the number. In general, the binary number system is used in computers. However, the octal, decimal and hexadecimal systems are also used sometimes.

Decimal Number System

Decimal number system has base 10 as it uses 10 digits from 0 to 9. In decimal number system, the maximum value of a digit is 9 and the minimum value of a digit is 0. The position of each digit in decimal number represents a specific power of the base (10) of the number system. Each position represents a specific power of the base (10). For example. The decimal number 1457 consists of the digit 7 in the units position, 5 in the tens place, 4 in the hundreds position, and 1 in the thousands place whose value can be written as:
(1×103) + (4×102) + (5×101) + (7×100)
(1×1000) + (4×100) + (5×10) + (7×1)
1000 + 400 + 50 + 7
1457

(1 x 1000)+ (2 x 100)+ (3 x 10)+ (4 x l)
(1 x 103)+ (2 x 102)+ (3 x 101)+ (4 x l00)
1000 + 200 + 30 + 4
1234

Binary Number System :-

The base 2 number system is called the Binary number system . It has only two digits '0' and '1' so its base is 2.
Binary Number: 101012

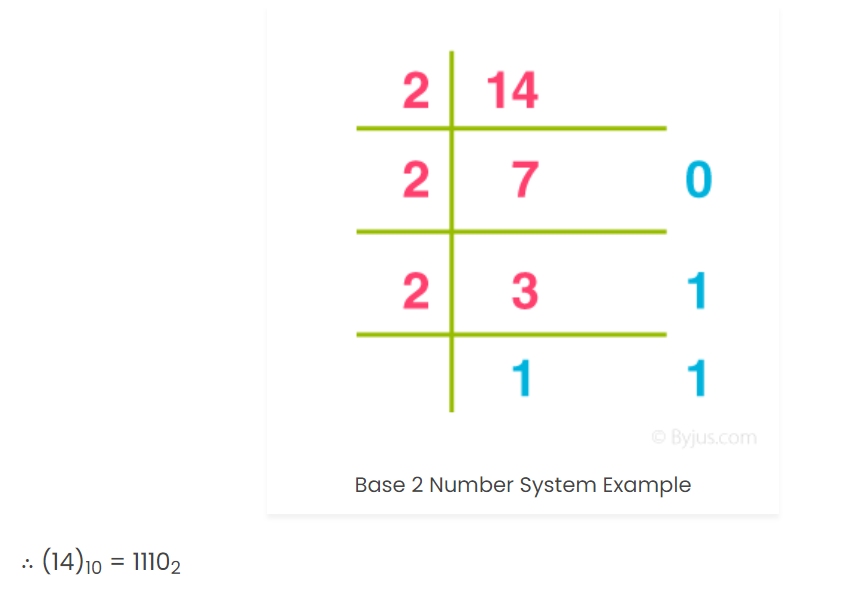
Example :- 14

(14)10 = 11102

Example :-


Octal Number System :-

In the octal number system, the base is 8 and it uses numbers from 0 to 7 to represent numbers. Octal numbers are commonly used in computer applications.
  • Uses eight digits, 0,1,2,3,4,5,6,7
  • it is Also called as base 8 number system.
  • Each position in an octal number represents a 0 power of the base (8). Example 80
  • Last position in an octal number represents a x power of the base (8). Example 8x where x represents the last position - 1

    • Example: Convert 2158 into decimal.

    2158 = 2 × 82 + 1 × 81 + 5 × 80
    = 2 × 64 + 1 × 8 + 5 × 1
    = 128 + 8 + 5
    = 14110

    Hexadecimal Number System :-

    In the hexadecimal system, numbers are written or represented with base 16. In the hexadecimal system, the numbers are first represented just like in the decimal system, i.e. from 0 to 9. Then, the numbers are represented using the alphabet from A to F.

    Example:- Convert hexadecimal 2C to decimal number.

    We need to convert 2C16 into binary numbers first.
    2C → 00101100
    Now convert 001011002 into a decimal number.
    101100 = 1 × 25 + 0 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20
    = 32 + 8 + 4
    = 44

  • Uses 10 digits and 6 letters, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
  • Letters represent the numbers starting from 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15
  • Also called as base 16 number system
  • Each position in a hexadecimal number represents a 0 power of the base (16). Example, 160
  • Last position in a hexadecimal number represents a x power of the base (16). Example 16x where x represents the last position - 1

    • Hexadecimal Number: 19FDE16

    ((1 x 164) + (9 x 163) + (F x 162) + (D x 161) + (E x 160))10
    ((1 x 164) + (9 x 163) + (15 x 162) + (13 x 161) + (14 x 160))10
    (65536+ 36864 + 3840 + 208 + 14)10
    10646210
    Note − 19FDE16 is normally written as 19FDE.





    Previous Next


    Trending Tutorials


    PHP

    PHP

    100+ Tutorials
    oops

    PHP OOPs

    80+ Tutorial
    Codeigniter

    Codeigniter

    100+ Tutorial
    Laravel

    Laravel

    100+ Tutorials
    Node.js

    NODE.JS

    100+ Tutorials
    Javascript

    Javascript

    100+ Tutorials


    Review & Rating

    0.0 / 5

    0 Review

    5
    (0)

    4
    (0)

    3
    (0)

    2
    (0)

    1
    (0)

    Write Review Here


    Most Popular Tutorials

     Important Link